Was ist Solver? Solver ist ein Werkzeug von Excel, das hilft uns eine optimale Lösung für ein Entscheidungsproblem zu finden. Es zeigt uns, welche Kombination von Einsatzfaktoren die Einnahmen maximiert oder die Ausgaben minimiert. Ohne Solver lassen sich die Aufgabenstellung nur mit mathematischen Kenntnissen oder ausprobieren lösen – wie praktisch!
Solver selbst ist nicht ganz so leicht zu versehen, da es kleinere und unendlich komplexe Berechnungen möglich macht. Für unser Tutorial geht es um einen Bauernhof oder besser um einen Bauern, der sich entscheiden muss, ob er Enten, Hühner oder Rinder aufzüchten will. Sie alle benötigen unterschiedlich viel Platz auf seinem Hof und erzeugen unterschiedlich viel Kosten. Der Bauer hat nur begrenzte finanzielle und räumliche Kapazitäten, weshalb er sorgsam abwägen muss, teure Rinder oder kleine Hühner zu beschaffen, um sein Ziel zu erreichen: den größtmöglichen Profit.
Hinweis: Die Beispielrechnung ist nicht realistisch und soll zeigen, wie Solver arbeitet.
Inhalt
Solver installieren
Lösung finden mit Solver (mit Beispiel)
Solver installieren
Solver ist nicht in der Standard-Excel-Version integriert und muss nachinstalliert werden, was relativ einfach und kostenlos funktioniert.
1. Wir klicken auf die Registerkartei Datei um die folgende Ansicht zu gelangen. Hier navigieren wir auf die Optionen ganz unten.
2. Es erscheint das Excel-Optionen-Dialogfenster und wir wählen im Menü die Einstellung Add-Ins.
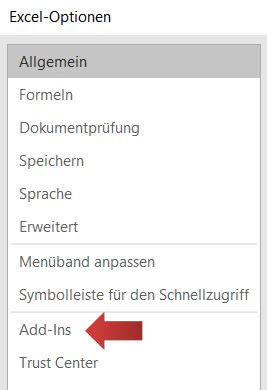
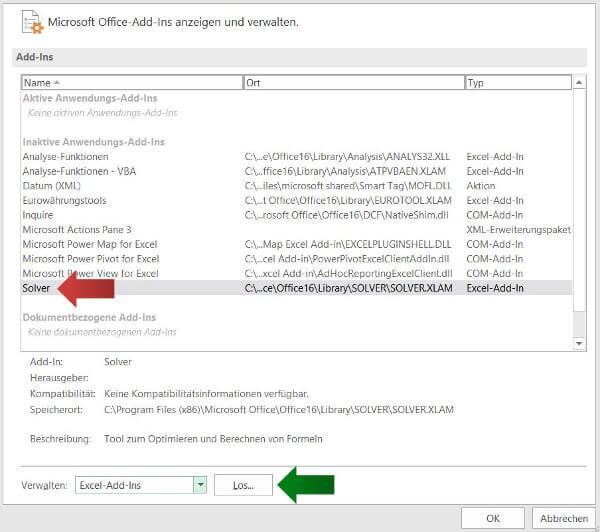
3. Nun können wir alle Add-Ins verwalten. Wir markieren mit einem Klick Namen Solver in der Liste und drücken anschließend den »Los… Knopf« weiter unten (grüner Pfeil).
4. Als Nächstes setzen wir in der Liste einen Hacken bei Solver und drücken OK.
5. Mit ein wenig Geduld warten wir die Installation ab.

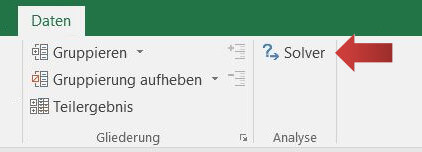
6. In der Registerkartei Daten befinden sich nun die Gruppe Analyse mit der Solver-Schaltfläche. Mit einem Klick auf die Schaltfläche gelangen wir zum Solver-Dialogfenster. Aber das wird erst mit dem nächsten Kapitel gezeigt.
Lösung finden mit Solver
Hinweis: Bevor du dieses Beispiel durchgehst, solltest du sicherstellen, dass Solver auf deiner Excel-Version korrekt installiert ist.
Zurück zu unserem Bauern und sein Problem. Die Fragen lauteten:
“Wie viele und welche Tiere soll sich der Bauer beschaffen, damit sein Profit maximiert wird?”
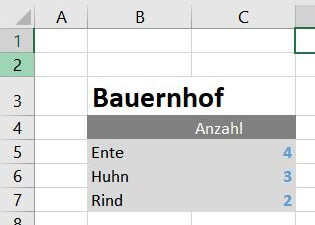
1. Damit Excel diese Frage später beantworten kann, legen wir eine Tabelle mit einer Auflistung für jedes Tier an. Ganz wichtig: in den Feldern Anzahl (in unserem Beispiel C5, C6, C7) dürfen nur Zahlen stehen. Tiere sind in unserem Beispiel der Inputfaktor. Für den Anfang genügt es, beliebige Zahlen als Platzhalter einzufügen, Excel wird später diese Ergebnisse überschreiben. In unserem Beispiel schreiben wir 4,3 und 2 als Platzhalter in die Zelle.
2. Als Nächstes erstellen wir eine Tabelle mit allen Parametern für unsere Entscheidung wichtig sind. Wir listen wieder alle Tiere auf und schreiben zu jeder Tierart, wie viel Fläche [Quadratmetern] benötigt, Kosten [Euro] verursacht und Geld erlöst wird. Diese Zahlen sind wichtig, damit wir berechnen können, welche Kombination aus verschiedenen Inputfaktoren (Tiere) den maximalen Profit ermöglicht. Wir sehen in unserem Beispiel, dass ein Rind viel mehr Platz (10 m²) als eine Ente (2 m²) benötigt, im Unterhalt wesentlich teurer (Kosten) ist, aber dafür wesentlich mehr Geld einbringt.
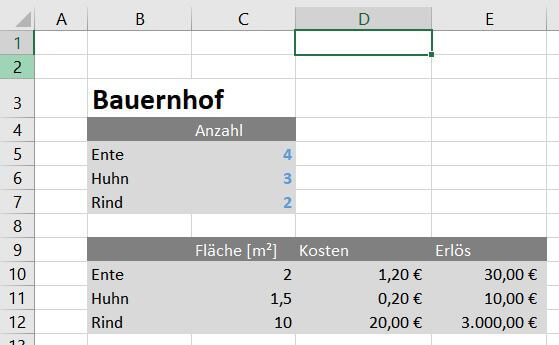
Hinweis: In der Regel sind die Inputfaktoren so aufgeteilt, dass jede Auswahl ihre Vor- und Nachteile hat. In unserem Beispiel sind Rinder groß, teuer aber wertvoll, Hühner günstig und klein, wohingegen Enten ein Mittelweg darstellen. Falls es einen offensichtlichen Favoriten gibt, der in allen Belangen am besten ist, benötigen wir keine Solver-Rechnung, weil die Entscheidung trivial ist: den Favoriten produzieren – so oft wie möglich. Solver wird angewandt, wenn die offensichtliche Lösung nicht erkennbar ist.
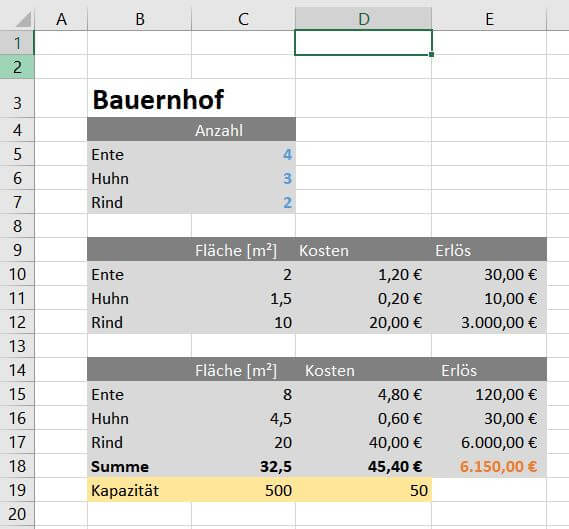
3. In der dritten Tabelle berechnen wir den tatsächlichen Verbrauch unserer Ressourcen, indem wir die pro Tier angaben aus der zweiten Tabelle mit der Anzahl der Tiere aus Tabelle 1 multiplizieren. Beispiel: In Zelle C15 wird C5xC10 gerechnet, bzw. Anzahl der Enten multipliziert mit der Fläche pro Ente. Bei 4 Enten und jeweils 2 m² benötigen wir 8m². In Zelle D16 berechnen wir die Kosten pro Tag für ein Huhn, in dem wir per Formel C6 (Anzahl Hühner) mit D11 (Kosten für ein Huhn) multiplizieren.
Unten summieren wir alle Flächen, Kosten und die Erlöse wie in Zeile 18. Unter jede Spalte tragen wir in Zeile 19 unsere Kapazitäten ein. Der Bauer hat schließlich nicht unendlich viel Platz und Geld. In unserem Beispiel hat der Bauer 500 m² Platz und nur 50 € am Tag für die Tiere.
Die Zelle E18 ist besonders hervorgehoben, weil dieser Wert (Gesamterlöse) optimiert werden soll (Zielfunktion).
Mit dieser Struktur können wir bei den Bedingungen in Tabelle 2 und den Häufigkeiten aus Tabelle 1 sofort die Auswirkungen auf unser Ergebnis sehen. Wenn wir die Platzhalter aus Tabelle eins ändern, so verändern wir automatisch unser Ergebnis. Mit Solver wird uns Excel eine Kombination von Hühnern, Enten und Rindern liefern, bei dem die meisten Verkaufserlöse erzielt werden.
4. Wir klicken in der Registerkartei Daten auf die Schaltfläche Solver.

5. Es öffnet sich das Solver-Parameter-Dialogfenster. In diesem Tutorial gehen wir jeden Wert einzeln durch und erklären Schritt für Schritt die Einrichtung der Solver Parameter.
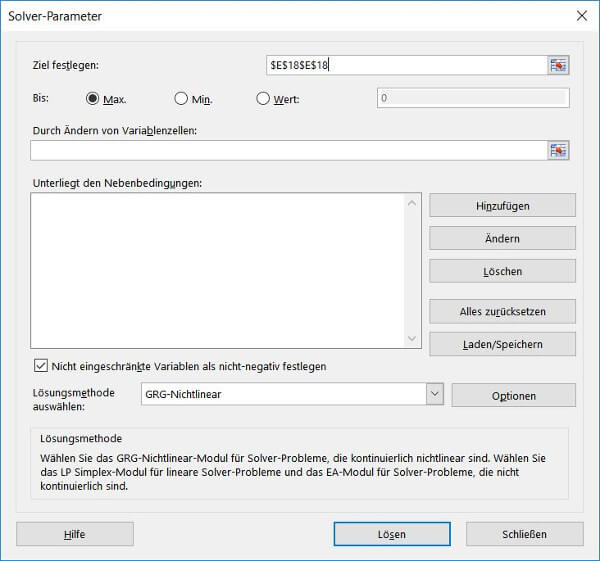
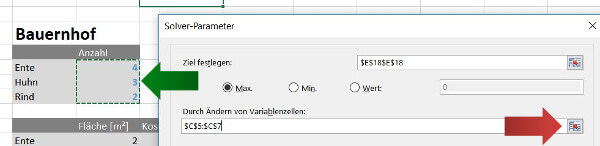
6. Bei Ziel festlegen klicken wir einmal auf das Eingabefeld und wählen unsere Zielfunktion (Gesamterlöse) in Zelle E18. Da wir unsere Umsätze maximieren möchten, wählen wir Max.
Bei einer Kostenfunktion bietet es sich an, einen möglichst keinen Wert zu ermitteln und Min. zu wählen. Solver kann auch einen bestimmten Wert errechnen, wobei hier mehrere Kombinationen aus den Einsatzfaktoren als Ergebnis möglich sein können.
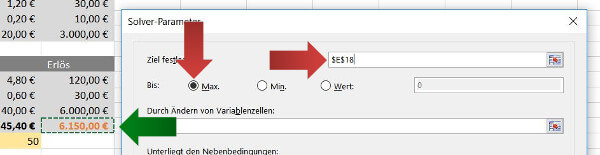
7. Im nächsten Schritt zeigen wir Excel die Variablenzellen mit den Inputfaktoren. Mit einem Klick auf das Symbol (roter Pfeil) können wir den Bereich C5 bis C7 (grüner Pfeil) markieren. Jetzt kennt Excel die Stellen, die manipuliert werden können. Alle anderen Zahlen in unserer Tabelle sind immer nur die Auswirkung von der Tierhäufigkeit.
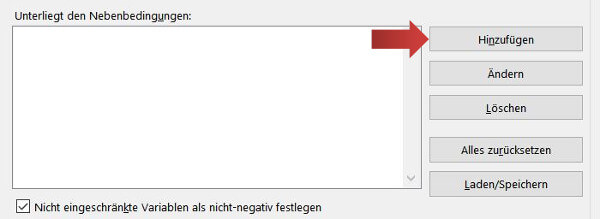
8. Kommen wir zu den Bedingungen. Wir können nicht unendlich viele Hühner und Enten auf den Bauernhof bewirtschaften und sind an unsere Kapazitäten gebunden. Damit diese in der Solver Rechnung berücksichtigt werden, fügen wir in dem Bereich »Unterliegt Nebenbedingungen« alle Bedingungen ein. Hierzu klicken wir auf die Schaltfläche Hinzufügen.
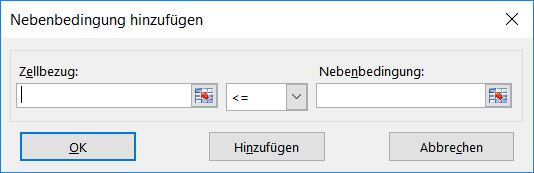
8. Es öffnet sich ein Nebenbedingung »hinzufügen-Dialogfenster«. Links geben wir den Zellbezug ein in der Mitte eine mathematische Gleichung und rechts die Nebenbedingung. An dieser Stelle müssen wir sehr sorgsam arbeiten und keine Fehler machen, da sonst die Solver-Berechnung falsche Ergebnisse liefert.
9. Die erste Nebenbedingung ist, dass die Summe aller Flächen nicht größer als unsere Kapazität für Flächen sein darf. Alle Ergebnisse unter der Kapazität sind machbar, alles darüber nicht umsetzbar. Aus diesem Grund wählen wir in Zellbezug die Zelle C18 mit der Summe aller verwendeten Flächen, als Gleichung wählen wir “kleiner oder gleich” (<=) aus und die Nebenbedingung ist die verfügbare Gesamtfläche in C19. Um die Nebenbedingung zu bestätigen klicken wir auf OK.
Da wir noch weitere Bedingungen aufstellen, klicken wir auf hinzufügen, um sofort die nächste Nebenbedingung zu erstellen. Die nächste Nebenbedingung ist, das die Summe aller Kosten in D18 kleiner gleich der Kapazität in D19 sein muss.

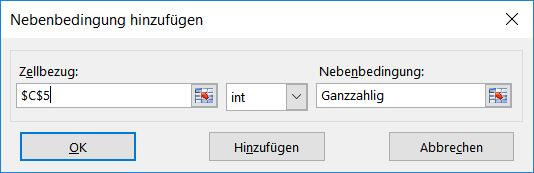
10. Dinge, die für uns völlig logisch sind, müssen hin und wieder Excel erst im Detail erklärt werden. Dies gilt auch für Solver-Berechnungen. Skrupellos wie Excel ist, hätte es keine Scheu uns 1,75 Rinder und 0,5 Enten als optimiertes Ergebnis zu präsentieren, was für unseren Bauern eher tragisch wäre, da eine halbe Ente einer toten Ente entspricht. Wir müssen Excel erklären, dass wir nur ganze Zahlen als Eingabe für unsere Tiere dulden. Deshalb fügen wir weitere Nebenbedingungen ein: Anzahl der Enten (c5) int Ganzahlig. Und das wiederholen wir für die Hühner und Rinder.
11. Am Ende haben wir 5 Nebenbedingungen, die Solver berücksichtigen wird.
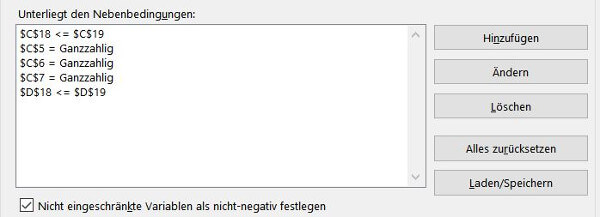
Hinweis: bei manchen Solverberechnungen sind noch weitere, vermeidlich logische, Nebenbedingungen sinnvoll. Zum Beispiel, dass alle Eingaben nicht nur ganzzahlig, sondern auch positiv sein müssen. Das gilt vor allem bei der Optimierung von Kostenfunktionen.
12. Wir klicken weiter unten auf den Knopf Lösen.
![]()
13. Wir klicken bei Ergebnisse auf OK.
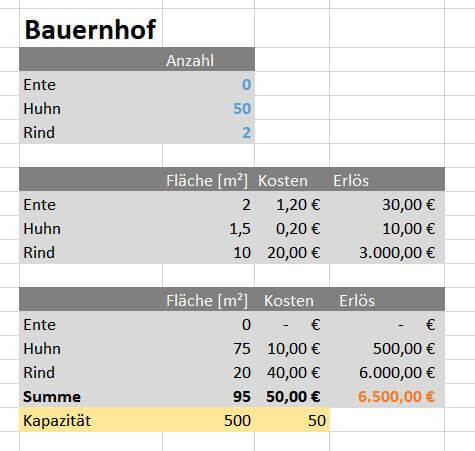
14. Und so sieht das optimale Ergebnis aus: 50 Hühner, 2 Rinder und keine Ente erwirtschaften 6.500 €. In Tabelle 3 können wir das Ergebnis näher untersuchen: wir sehen, dass die Fläche nur kaum ausgereizt wurde. Der Bauer wird nur 95m² von seinen 500 ² benutzen. Der Engpass war das geringe Tagesbudget von nur 50€. Er kann sich nicht mehr Tiere leisten. An dieser Stelle können wir den Bauern nur raten, das Tagesbudget zu erhöhen.
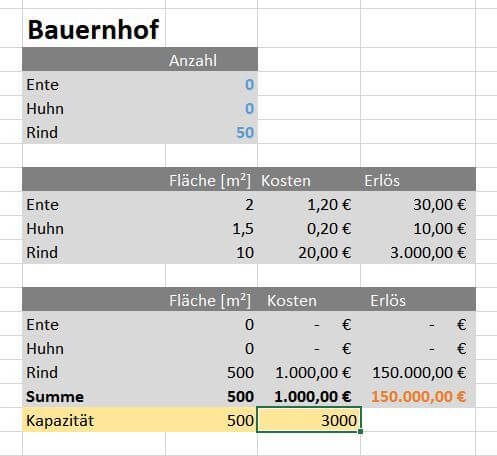
15. Angenommen der Bauer hat einen Bankkredit erhalten und jetzt mehr finanziellen Spielraum, wie würde das Ergebnis aussehen, wenn er nun 3.000 € pro Tag zur Verfügung hätte? Wir passen den Wert in Zelle D19 an und erhöhen auf 3.000. Jetzt führen wir die Solverrechnung wie erneut durch (Schritt 4). Die Einstellungen hat sich das System gemerkt, weshalb wir gleich auf lösen klicken.
Das neue Ergebnis: 50 Rinder und 150.000 € Umsatz, ein gewaltiger Unterschied zu den 6.500 € aus der vorherigen Rechnung.
Im Detail sehen wir, dass jetzt die Fläche der Engpassfaktor ist, jeder Quadratmeter wird für Rinder beansprucht. Der Kredit für den Bauer ist zu hoch, weil er in unserer Rechnung nicht mehr als 1.000 € pro Tag benötigt.
Die Zahlen wie “Kosten” und Beispielrechnungen sind stark vereinfacht, um dieses komplexe Thema möglichst simpel zu erklären.
Für gewöhnlich wird die Zielwertsuche nicht einfach auf den Erlösen angewendet. Es wird eine Gewinngleichung erstellt, die die Gesamterlöse mit den Gesamtkosten verrechnet. Diese Gewinngleichung ist die eigentliche Zielgleichung für die Solver-Optimierung. Fühle dich frei unser Beispiel mit einer Gewinngleichung zu bereichern und ein neues Ergebnis zu rechnen; oder gleich ein eigenes Beispiel zu erstellen. Wenn du das Prinzip der Solver-Berechnung verstanden hast, kannst du die Tabellen auch nach deinem belieben anordnen und musst dich nicht zu genau an dieses Beispiel halten.